Further, that he spends the night of December 24th circling the globe in a sleigh pulled by flying reindeer. That he gains access to the homes of children that celebrate Christmas children, and that he gives them presents. And that he does this in the dark, unseen.
Granted, it seems. impractical. Over the course of one night, St. Nick has to stop by the home of every Christian child in the world. Of which there are a lot - an indeterminately large number of kids waiting for their gifts.
I decided to figure out how many, how big a task Mr. Claus faces as he races west across the face of the globe, staying ahead of the sun. And I did. Or, anyway, I came up with a pretty solid estimate.
The Methodology
What I wanted to figure out is this: how many Christian children live in each general area of the world. The region is important: where the kids live impacts the feasibility of the thing. If kids are distributed evenly, Santa has all night to reach everyone; if they live in the same place, he has about half as long.
It's impossible to find this information without considering countries; no one tracks demographics based on longitude. So, for every country in the world - of which there are a lot - I really needed to figure out the population broken down by age, religion and time zone.
Thanks to the CIA, we can readily determine populations by age and religion, and, by combining the two measures, roughly approximate the number of Christians for any given age group. (For the purposes of our experiment, people 14-and-under receive presents from Santa.) Time zones are equally easy, via Wikipedia.
The equation is this: compare population of young people with density of Christianity and plot it on the globe. From that, you've got total population and the times at which Santa should hit them. I ignored the mechanics of distance between houses - after all, I can't know how many houses have multiple children, what regions are more densely packed, etc. The math, it seemed, should be easy.
Should be. Isn't. Before getting bogged down in the incredible nuance of the world's religions and time zones that went into determining these numbers, I'll share the end result.
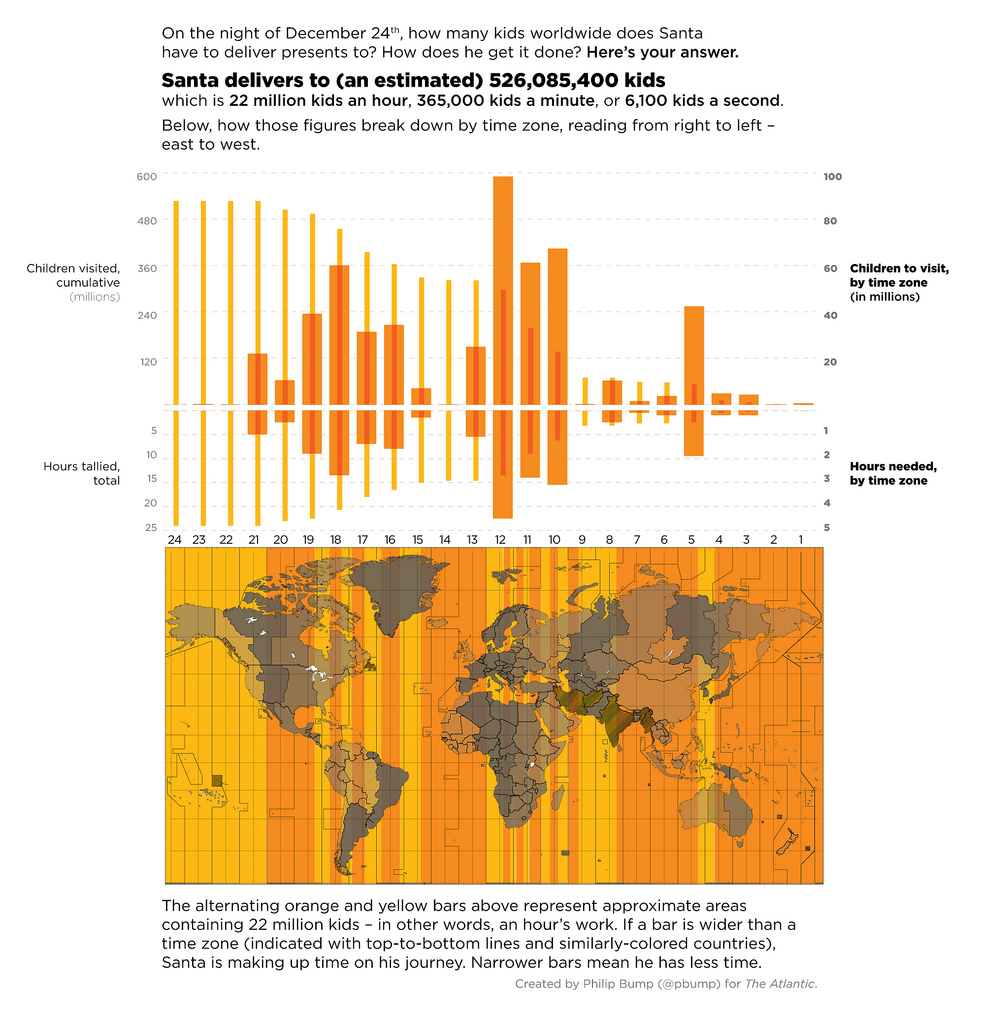
There are just over 526,000,000 Christian kids under the age of 14 in the world who celebrate Christmas on December 25th. In other words, Santa has to deliver presents to almost 22 million kids an hour, every hour, on the night before Christmas. That's about 365,000 kids a minute; about 6,100 a second. Totally doable.
Especially when you consider the uneven distribution of kids in the world. Santa needs to hit 22 million kids every hour. If Santa starts at the International Date Line and heads west, the first four time zones he passes barely contain that many kids waiting for presents. He's already got three hours in the bank. Until, you know, he gets to Europe, which kind of breaks his schedule.
Here's what Santa's night looks like. Read it from right to left; i.e., east to west.

The Caveats
As I said, the math was harder than it seemed. For your edification, here are the complexities and oddities I encountered - and which indicate you might want to take my calculations with a grain of salt.
Below, a time zone-by-time zone breakdown of Santa's trip west, delineating how many children Santa has to serve in each and how that compares to the total number of children in the region and the children awaiting presents in the world as a whole.
Over half a billion kids in the span of one night, all while distracting the experts at NORAD with gallivanting decoys. If anyone has ever deserved sainthood, it's Nick.
We want to hear what you think about this article. Submit a letter to the editor or write to letters@theatlantic.com.